Your Time has Finished
Loading...
Official TSA SDT Questions (2008-2019)
Your Score: %
Average Score of All Users:
You performed better than of students
Section Breakdown
| Your Score | Average of all Users | Percentile | |
|---|---|---|---|
| Official TSA SDT Questions (2008-2019) |
Official TSA SDT Questions (2008-2019)
Your score:
Average score:
You performed better than of students
Speed as well as accuracy is important in this section. Work quickly, or you might not finish the paper. There are no penalties for incorrect responses, only marks for correct answers, so you should attempt all questions. Each question is worth one mark.
Calculators are NOT permitted.
Here you will find all TSA SDT questions that have been written 2008-2019.
Steven has a customised motorcycle that he is very proud of and shows regularly in It is very important to him that his presentation is perfect and he likes to stop in front of the judges with both his tyre valves in the same position. The front tyre is smaller than the rear to aid its handling. The circumference of the front wheel is 2m and the circumference of the rear wheel is 2.5m.
Steven starts with both valves in the same position at the bottom of each wheel.
Explanation
The correct answer is D.
Find the lowest common multiple of 2 and 2.5. This is 10 which is D.
The roads on Bolandia all run either north – south or east – west and are laid out on a 5km Ahmed and Wayne are delivery drivers. One morning, Ahmed starts at Abbeytown and drives 5km west then 15km south to reach Barneyville. He then drives 5km east to Carloston. Wayne started at Barneyville, drove 5km south to Denburgh then 10km east and 15km north to Easterby. Ahmed then rings Wayne to arrange to meet for lunch.
Explanation
The correct answer is B.
For this question we can use Barneyville, a location that both drivers visit, to figure out how their end locations compare to each other. Jotting down a quick representation of their travels post Barneyville shows that either Ahmed will have to travel 5km east followed by 10km North, or Wayne will have to do the inverse, so drive 10km south followed by 5km west for them to meet. Therefore, the answer is B, 15km
Ionnais lives at the bottom of a very steep hill. Worse than that, the post office is at the Every Thursday he must go there to collect his pension. He can only walk at 2 km per hour uphill but manages 4 km per hour downhill. The round trip, excluding the wait at the post office, takes him 4½ hours.
Explanation
The correct answer is B.
Time=distance/speed. The total time is 4.5, which would be the sum of the times for going uphill and downhill, which would be equal to the distance/speed for each part of the journey. Since the distance travelled is the same uphill and downhill, we can represent the distance from home to the post office (or vice versa) as ‘y’. We can form an equation from Time=distance/speed: 4.5= y/2 + y/4 (where y/2 is the time taken uphill and y/4 is the time taken downhill). This can be simplified to 4.5=(2y+y)/4 and then to 4.5×4=3y, then 18=3y, so y=6, which is the distance from his house to the post office.
Starting from its depot in town X, a delivery lorry is to make deliveries to three towns A, B and C, in any order which the driver chooses and finally to return to X.
Straight roads connect each town to every other town.
Explanation
The correct answer is C.
 U
Medicmind Tutor
U
Medicmind Tutor
Tue, 25 Jul 2023 14:59:05
Can some explain this using a diagram please?
A man drives off from his house and travels through the village at a constant speed. As he leaves the village behind, his speed increases to a new constant value which he maintains until he reaches a steep hill which slows him down. At the top of the hill the driver stops for a few minutes to admire the view. He realises that he has left his picnic basket at home and so drives rapidly back along his route to collect it.
Explanation
The correct answer is D.
Initially the man drives at a constant speed, so the relationship between time and distance will be proportional, ie a straight line with a postive gradient; eliminate C as the first part of the graph is horizontal. His speed then increases, so the gradient will suddenly increase (the line will be steeper); eliminate B as the line becomes less steep. He then slows down upon reaching a steep hill, so the gradient will decrease; we cannot eliminate anymore graphs at this point. The driver then stops, so the graph will be horizontal; eliminate E because the graph has a negative gradient at this point. He then begins driving back home, so the gradient will be negative as he is getting closer to home; this is shown by graph D but not A, so D is the answer.
As part of a journey, I must travel from Bowbridge to Downland. I can choose either the motorway (known locally as ‘the road to hell’) or the old road known as Buttercup Way. On the motorway I average 60 mph, on the old road I average 40 mph. I can change from one to the other at Clatterton where they cross.
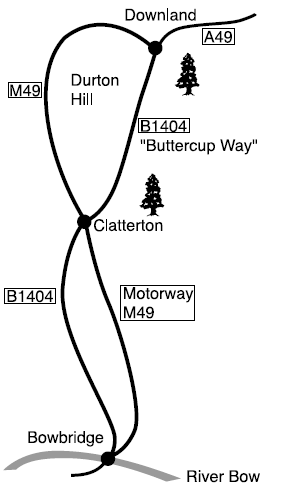
The distances by the two roads are as follows:

Explanation
The correct answer is C.
Calculate whether the motorway or Buttercup way would be the quickest for both Bowbridge to clatterton and from clatterton to downland. Do this by dividing the distance by the speed to get time. For Bowbridge to clatterton, on the motorway it would take: 35/60=7/12 hrs, whereas on Buttercup way it would take 30/40=9/12 hrs. 7/12<9/12, therefore it would take less time to travel on the motorway from Bowbridge to Clatterton. For Clatterton to Downland, on the motorway it would take 7/12 hrs again, whereas on Buttercup way it would take 20/40=6/12 hrs. 7/12>6/12, therefore it would take less time on Buttercup way from Clatterton to Downland. Therefor the fastest route would be on the motorway for the first part of the journey and then on Buttercup way for the second part, which would take: 7/12+6/12=13/12hrs. The slowest route would be the opposite (Buttercup way first and then the motorway) which would take: 9/12+7/12=16/12hrs. The difference between these is: 16/12-13/12=3/12=0.25hrs, which is 15 minutes.
Stewart and Michael have arranged to meet. Michael is about to set off on his bicycle, and at the same time Stewart is going to run to meet him.
Michael can cycle at a steady 20 kilometres per hour and Stewart can run at a steady 12 kilometres per hour. They live 8 kilometres from each other.
Explanation
The correct answer is A.
Image it is just 1 vehicle travelling the 8km. The speed of the vehicle would be the sum of the Stewart and Micheal’s speeds: 20+12=32km/h. To calculate the time, divide the distance by the speed: 8/32=1/4=0.25 hours. In minutes, this would be 0.25×60=15 minutes.
Sven is a keen cyclist and is riding from Alvros to Berget. At his normal cycling speed this will take him 30 minutes. His wife, Helga, will go by car to bring him and his bike back. They leave at the same time, but two thirds of the way between the two towns the car breaks down and Helga has to walk the rest of the way. The car goes at three times the speed Sven cycles. But Helga walks at only one third of the speed he cycles.
Explanation
The correct answer is C.
Since the car goes three times the speed that Sven cycles, this means that it will complete the journey in 3 times less the time. Since it takes Sven 30 minutes from Alvros to Berget, the car will therefore take just 10 minutes. The car breaks down two thirds of the way between, so Helga travels using the car for 10 x 2/3 = 6.66 minutes. The remaining 1/3 she walks. As she walks at 1/3 the speed that Sven cycles (so she is 3 times slower), this means that it will take her 3 times as longer to complete the full journey. So the complete journey (had she walked the whole way) would have taken her 30×3=90 mins. Since she is only walking a third of the way this means that she walks for 90/3=30mins. So overall while Sven completes the journey in 30mins, Helga takes 6.66+30 mins = 36.66 mins. This means that to the nearest minute, Sven arrives first by 7 minutes and the correct answer option is C.
The following table gives information about five different car models.
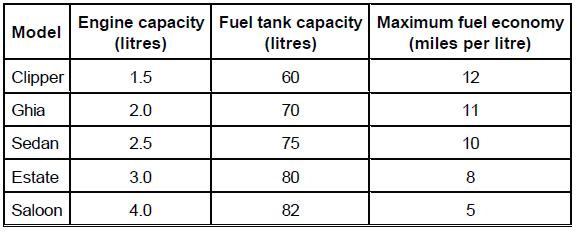
Explanation
The correct answer is B.
In these types of questions with tabular data, you are often given more data than is needed to answer the question. It is therefore important to clearly read the question and identify the data you need to focus on. Here, to figure out which model will travel furthest on a full tank, you only need to focus on the Fuel tank capacity and maximum fuel economy. The correct answer will be the model that has the highest product when these values are multiplied together. We can quickly rule out options such as the Clipper and Saloon as we can see that these will not give the largest product without having to actually calculate it. From the remaining options, we can see that Ghia has the highest product (70 x 11 =770 miles within a full fuel tank – compared to 750 for the Sedan and 640 of Estate). Therefore the correct answer option is B Ghia.
Last month, in an attempt to improve my fitness, I began to run The maximum distance I have time to fit in on any particular day is 8 miles, but my aim is to maintain an average of at least 5 miles per day.
After 15 days my average was just under 6 miles per day, then the following day I increased my average to just over 6. Since then (for the last 9 days, up to and including today) I have been able to run only 2 miles each day.
Explanation
The correct answer is B.
 U
Medicmind Tutor
U
Medicmind Tutor
Tue, 25 Jul 2023 15:00:07
Does anyone have an explanation for this?
 Delon
Medicmind Tutor
Delon
Medicmind Tutor
Sat, 28 Sep 2024 19:38:17
https://www.youtube.com/watch?v=FT-1B63DB3E For Solution. I did it as a timeline to calculate total mi compared to days. From running total 114 mi on day 25, we want the average greater than 5: 114+8n/25+n (n being days, 8 is maximum distance). You will triangulate on 4 by trying a couple quick multiplications, or you can times out the above division to calculate n = 11/3
Central Avenue is a long straight road, several kilometres Both my home and my office are on Central Avenue, and the diagram below shows their positions, together with two sets of traffic lights that lie in between.

Both sets of lights turn to green for Central Avenue traffic simultaneously, showing green for exactly two minutes, turning green again exactly two minutes later.
I cycle to work every morning at a steady speed of 5 metres per second (except, of course, whilst waiting at traffic lights).
Explanation
The correct answer is D.
The first 400m would take 400/5=80seconds. To maximise the journey time, we must maximise the time spent waiting at traffic lights. So let’s assume the first set of traffic lights turn red just as the person reaches them after travelling 400m. So the person would spend 2 minutes=120 seconds stationary there. The following 900m would take 900/5=180seconds=3minutes. During the first 2 minutes travelling the 900m stretch, the traffic lights would be green (as they have just spent two minutes being red). During f the 3rd minute, they would be red. So when the person reaches the second set of traffic lights, they would be just starting their second minute of being red. Therefore the person would have to wait here for 1minute before travelling the final 500m, which would take 500/5=100seconds. In total, the journey time would be: 80+120+180+60+100=540seconds which is equal to 540/60=9 minutes.
Sue takes her dog Freya to the She throws a stick for Freya to fetch. Freya runs to collect the stick and bring it back to Sue. While Freya is collecting the stick, Sue walks slowly towards Freya.
Explanation
The correct answer is B.
The distance between Sue and Freya initially increases, because Freya is moving faster than Sue, so the initially gradient of the graph must be positive, so A and C can be eliminated. Then the distance between them will decrease, as Freya runs back to Sue whilst Sue us walking towards Freya, so the gradient will then be negative, so E can be eliminated. This leaves B and D, which differ because B shows that the distance between them increases slower in the first stage than when the distance between them decreases in the second stage (as the second part of the graph is steeper/ the magnitude of the gradient is greater). Whereas, graph D shows the opposite. B is the correct answer because the distance between them will decrease faster as both Sue and Freya are moving towards each other, unlike when the distance between them is increasing (because in this stage Sue is moving towards Freya and Freya is moving away from Sue rather than both of them moving away from each other).
David has a new cycle computer but has not learned all the functions yet, so can only read the cumulative mileage and average speed of all of the journeys since he fitted it. On his first journey using it he covered 15 km at an average speed of 30 km/h. He can work out from this that the journey took him 15/30 hours or exactly 30 minutes. After the second journey, his cumulative mileage was 24 km and overall average speed 32 km/h.
Explanation
The correct answer is D.
Total time= total distance/average speed= 24/32=0.75hours. Time taken in 2nd part of journey=total time- time taken in 1st part of journey= 0.75-0.5=0.25hours. Distance travelled in 2nd part of journey= total distance- distance travelled in 1st part of journey= 24-15=9km. Speed during 2nd part of journey=distance/time= 9/0.25=36km/h.
 d
Medicmind Tutor
d
Medicmind Tutor
Mon, 24 Jul 2023 14:27:33
d
This diagram shows the roads that connect four towns and the distances involved.
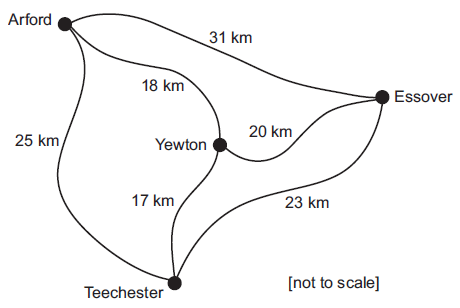
I live in Essover. This afternoon I have to visit clients in Arford, Teechester and Yewton before returning to Essover. It does not matter in which order I visit the clients.
Explanation
The correct answer is C.
Given that the 31km journey from Essover to Arford is the longest journey shown, we want to avoid it as much as possible. So starting from Essover we can either go to Yewton or Teechester. As we will see, either option will lead to the same outcome, as in order to avoid the 31 km journey and to also avoid doubling back we will use one to start of the visit and the other to return and it does not matter which way round we go about it. Say we take the 20 km route to Yewton first, we now have the option of travelling to Teechester or Arford. The former option will lead to us then going to Arford and then using the 31km road which is pretty long, so it’s much better to travel to Arford from Yewton instead. Now we can travel to Teechester and use the 23km route back to Essover, giving us a total of 20+18+25+23=86km. The result will be the same if we were to do the inverse, i.e. Essover-Teechester-Arford-Yewton-Essover. So, the correct answer is C.
Rosie needs to mow her lawn. She has just bought a new lawn mower, and believes she can mow at a rate of 2m² a minute. With her old mower, she could only mow the lawn at a rate of 1 m² a minute. Her lawn is 10m by 25m. There is a patio in one corner which is 2m by 3m and which she does not need to mow.
Explanation
The correct answer is A.
The area of her lawn is (10 x 25) – (2 x 3) = 250 – 6 = 244m^2. As her previous mower would allow her to mow at a rate of 1m^2 per minute, she would complete the lawn in 244 mins. Her new one is twice as fast and will allow her to complete the lawn in half the time so 244/2 = 122mins. The difference between these two timings is 122mins (244-122) so the answer is A.
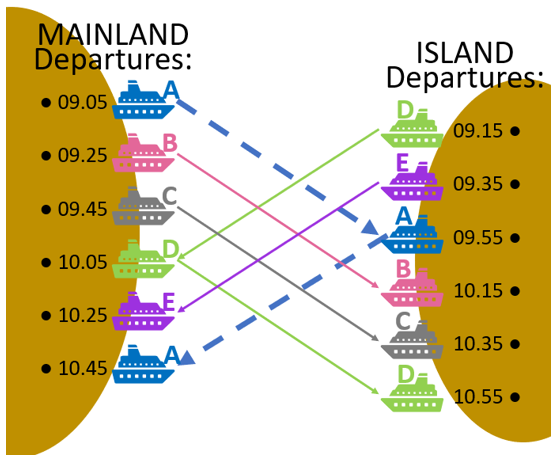
Fergus Castle is a tourist attraction on a small island off the coast of the mainland. A ferry service runs between the mainland and the island, and takes 40 minutes to make a single journey in either direction. There is a turnaround time of 5 minutes at the end of each single journey. Each day, ferries leave the mainland every 20 minutes, at 5, 25 and 45 minutes past each hour, starting at 09:05. Ferries leave the island at 15, 35 and 55 minutes past each hour, starting at 09:15.
Explanation
The correct answer is C.
The first ferry (Ferry A) that leaves the mainland at 09.05 will take 40 minutes to travel to the island, followed by the 5 minute turnaround time at the end of the journey, so it will be ready to make the journey back from the island by 09.50, which means that it can do the 09.55 departure from the island. It will take a further 45 minutes before it returns to the mainland and is ready to make the next journey, meaning that it will be ready by 10.40 and can take the 10.45 departure from the mainland. In the meantime, 4 other ferries will have to leave the mainland for the 09.25, 09.45, 10.05, 10.25 departures, as the initial ferry (Ferry A) would be partway through its journey and therefore unable to make these departure times. Therefore at least 5 ferries are required. If we consider the departures from the island that occur prior to the 9.55 departure that Ferry A will complete (so the 09.15 and 09.35 departures that leave the island) we realise that two additional ferries are not required for these, as the 09.15 island departure will be able to return to the mainland by 09.55 and after its 5 minute turn around, it will be ready for the 10.05 departure from the mainland, hence, it’s the same ferry as 10.05 mainland departure. Similarly, the 09.35 departure from the island can make 10.25 mainland departure, so an additional ferry is not required and therefore the minimum number of boats required is 5 and the correct answer is C. It is not necessary to consider later time points as this pattern will continue.
A car journey begins with a 15 km drive at an average speed of 60 km /hour, then 5 hours on the motorway, including two 15-minute rest stops, travelling at an average driving speed of 80 km / hour, and finally a 20 km drive at an average speed of 40 km /hour from the motorway to the destination.
Explanation
The correct answer is D.
First calculate the time that the journey took. First segment: 15km at 60km/hour = 15minutes. Second segments: 5 hours (note that this includes the 15-minute stops). Final segment: 20 km at 40km/hour = 30 minutes. Add all that together to get 15mins+5 hours+30 mins = 5 hours 45 mins. Hence the correct answer is D as 5 hours and 45 mins before 12 noon is 6.15 am.
Three friends are training to run a marathon. Part of this training involves running steadily round a track in the local park. They are all at different stages in their training schedules so they run at different speeds. Alec completes each lap in 3 minutes, Barry takes 5 minutes and Colin takes 6 minutes.
They all leave the start line at the same time.
Explanation
The correct answer is B.
For this question, first calculate the time until they all cross the start line together. This will have to be the lowest common multiple of 3, 5 and 6. As any multiple of 6 is already a multiple of 3, we can ignore 3 and find the lowest common multiple of 5 and 6, which is 30. So, the three of them will cross the start line after 30 mins. Since Alec takes 3 mins per lap, he will have completed 30/3= 10 laps by that point, whereas Barry will have completed 30/5 = 6 laps. So, Alec completes 4 more laps than Barry. Top Tip – read the question carefully, as they will often have answer options meant to mislead you. Here, if you simply calculated the total laps completed by Alec, which is 10, you can see a corresponding answer option (E) is there to catch you out.
Official TSA SDT Questions (2008-2019) Review Screen
Instructions
Below is a summary of your answers. You can review your questions in three (3) different ways.
The buttons in the lower right-hand corner correspond to these choices:
1. Review all of your questions and answers.
2. Review questions that are incomplete.
3. Review questions that are flagged for review. (Click the 'flag' icon to change the flag for review status.)
You may also click on a question number to link directly to its location in the exam.
Official TSA SDT Questions (2008-2019) Section
Final Answer Review Screen
Instructions
This review section allows you to view the answers you made and see whether they were correct or not. Each question accessed from this screen has an 'Explain Answer' button in the top left hand side. By clicking on this you will obtain an explanation as to the correct answer.
At the bottom of this screen you can choose to 'Review All' answers, 'Review Incorrect' answers or 'Review Flagged' answers. Alternatively you can go to specific questions by opening up any of the sub-tests below.
Official TSA SDT Questions (2008-2019) Section
TI-108